setelah dari kemaren ngepost tentang makanan, skrg tak coba ngepost tentang sedikit pelajaran stastistik yg ada di mata kuliah teknik oemodelan dan simulasi. jadiii, klo dalam pemodelan dan simulasi, ada suatu cara yang dipake buat memperkirakan terjadinya peluang yang biasa disebut dengan Distribusi Probabilitas. distribusi inii dipake buat suatu simulasi yang mempunyai data yang tidak tetap. disini saia coba buat jelasin yang lebih khususnya yaaa.....
Distribusi Probabilitas dalam Simulasi Sistem Diskret
Kunci aplikasi probabilitas dalam statistic adalah memperkirakan terjadinya peluang/probabilitas yang dihubungkan dengan terjadinya peristiwa dalam beberapa keadaan. Jika kita mengetahui keseluruhan probabilitas dari kemungkinan yang akan terjadi, seluruh probabilitas kejadian tersebut akan membentuk suatu distribusi probabilitas. Distribusi probabilitas banyak digunakan dalam simulasi sistem diskret terutama dalam simulasi sistem antrian (queueing system). Distribusi probabilitas dapat dijelaskan melalui fungsi kepadatan atau fungsi distribusi kumulatif.
naaah, saia jelasin 5 Distribusi yang umum digunakan yaaa.....
1. Distribusi Poisson
Distribusi ini pertama kali diperkenalkan oleh Siméon-Denis Poisson (1781–1840) dan diterbitkan bersama teori peluangnya, pada tahun 1838 dalam karyanya Recherches sur la probabilité des jugements en matière criminelle et en matière civile (“Penelitian Peluang Hukum Masalah Pidana dan Perdata”). Karyanya memfokuskan peubah acak N yang menghitung antara lain jumlah kejadian diskret (kadang juga disebut "kedatangan") yang terjadi selama interval waktu tertentu. Apabila nilai harapan kejadian pada suatu interval adalah λ , maka peluang terjadi peristiwa sebanyak x kali adalah
Ciri-ciri dari distribusi Poisson :
- Banyaknya hasil percobaan yang satu tidak tergantung dari banyaknya hasil percobaan yang lain.
- Probabilitas hasil percobaan sebanding dengan panjang interval waktu.
- Probabilitas lebih dari satu hasil percobaan yang terjadi dalam interval waktu yang singkat dalam daerah yang kecil dapat diabaikan.
Distribusi Poisson digunakan dalam :
- Menghitung probabilitas terjadinya peristiwa menurut satuan waktu, ruang atau isi, luas, panjang seperti: Banyaknya penggunaan telpon per menit, banyaknya kesalahan ketik per halaman sebuah buku, banyaknya mobil yang lewat selama 5 menit di suatu ruas jalan, dsb.
- Menghitung disktribusi binomial apabila n-besar (n ≥ 30) dan p relatif kecil (p < 0,1)
2. Distribusi Eksponensial
Distribusi probabilitas eksponensial merupakan pengujian yang dilakukan untuk melakukan perkiraan atau prediksi dengan hanya membutuhkan perkiraan rata-rata populasi, karena distribusi eksponensial memiliki standar deviasi sama dengan rata-rata. Distribusi ini termasuk ke dalam distribusi kontinyu. Ciri dari distribusi ini adalah kurvanya mempunyai ekor di sebelah kanan dan nilai x dimulai dari 0 sampai tak hingga. Distribusi eksponensial merupakan model waktu (atau panjang atau area) antara kejadian Poisson. Dengan fungsi pdf dan cdf sebagai berikut :
Sedangkan mean dan varians dari distribusi eksponensial adalah sebagai berikut :
Gambar kurva distribusi eksponensial berbeda-beda tergantung dari nilai x dan λ sebagai berikut :
3. Distribusi Erlang
Distribusi Erlang dikembangkan oleh A. K. Erlang untuk menguji jumlah panggilan telepon yang mungkin dilakukan dalam satu waktu pada suatu switching station milik operator. Distribusi ini bekerja pada perencanaan trafik telepon yang pemakaiannya meluas agar dapat menghitung waktu tunggu dalam system antrian secara umum. Distribusi Erlang kini digunakan dalam proses stochastic.
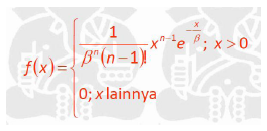
Berikut ini merupakan probability density function dari distribusi Erlang :
Sedangkan mean dan varians dari distribusi Erlang adalah sebagai berikut :
Rataan (Mean) :
Varians :
Contoh Kurva Distribusi Erlang :
4. Distribusi Hiper-Eksponensial
Distribusi Hiper-Eksponensial terjadi dalam teori antrian ketika waktu pelayanan untuk satu unit berdistribusi eksponensial dengan jumlah parameter lebih dari satu. Berikut ini merupakan probability density function dari distribusi Hiper-Eksponensial :
5. Distribusi Normal
Distribusi Normal adalah suatu distribusi empirik atau teoritis, yang meskipun sudah banyak digunakan dalam bidang statistik tetapi masih merupakan suatu misteri pada banyak orang. Distribusi Normal disebut juga distribusi Gauss ( Carl Friedrich Gauss, seorang ahli matematik yang banyak memberikan andil pada pengembangannya pada permulaan abad 19). Kata 'normal' disini tidak diartikan sebagai kata-kata dalam bahasa inggris 'normal' yang berarti 'ordinary atau common' dan tidak juga seperti terminologi kedokteran sebagai 'tidak sakit',, namun merupakan suatu model matematik yang menggambarkan penyebaran probabilitas dari pengamatan yang tidak terbatas dan diukur terus menerus.Ciri-ciri dari distribusi normal adalah sebagai berikut :
- Grafiknya selalu ada di atas sumbu datar X
- Bentuknya simetrik terhadap x = μ
- Mempunyai satu modus
- Grafiknya mendekati sumbu datar x dimulai dari x = μ + 3σ ke kanan dan x = μ - 3σ ke kiri
- Luas daerah grafik selalu sama dengan satu unit persegi
- σ makin besar, kurva makin rendah (B)
- σ makin kecil, kurva makin tinggi (A)
Sedangkan mean dan varians dari distribusi Normal adalah sebagai berikut :
Rataan (Mean) :
Varians :
Contoh Kurva Distribusi Normal :
materi inii gw dapetin dari berbagai sumbeer, hehehe :) maaf klo kurang lengkap. untuk studi kasus nyaa, coba dicari" dulu ajaa yaaa.... selamaat belajaar!!!









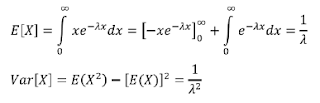










4 comments:
thanx y sist
bermanfaat mas. keep on working!
bisaa buktii rataan dan varian utk dstribusi weibull gk ni? bntu dong
mksih
ka bisa minta pembuktian untuk distribusi eksponensial nya🙏
Post a Comment